
Latest acceleration tests using plasma waves excited by a 350 pC electron beam (driver) generated by the SPARC_LAB photo-injector have produced the first significant results.
During the last run, the acceleration of a second beam (witness) of 20 pC was obtained with an energy gain of about 6 MeV and an energy spread of about 0.2%. The accelerating field is produced by the plasma contained in a 3 cm-long and 1 mm diameter capillary, shown in Figure 1. The driver precedes the witness by 1 picosecond and the plasma is produced by ionizing hydrogen with an high voltage discharge.
The main difficulty in this type of experiment is represented by the size of the “accelerating cavity” created in the plasma. Considering a plasma density of 2×1015 cm-3 (which corresponds to a plasma wavelength of about 700 microns), the region useful for acceleration has an effective length of less than 300 microns and a radius of a few tens of microns. The electron beams must therefore have dimensions well below these values. To give an idea of the difficulty, just think that a human hair has a diameter of only 100 microns.
In the SPARC_LAB experimental setup, the two beams are generated directly from the cathode and then compressed in the first accelerating section. The beams, with an initial energy of 89.8 MeV, are then focused in the capillary by a triplet of permanent-magnet quadrupoles. The witness has an initial relative energy spread of 0.2%.
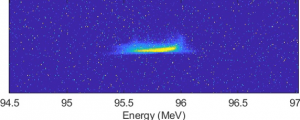
Figure 2 shows a plasma-accelerated witness with 95.8 MeV final energy. The overall energy gain is thus 6 MeV. Since the capillary is 3 cm long, the resulting accelerating gradient is about 200 MV/m. The final goal is to reach the threshold of 1 GV/m.
There are two typical issues of this acceleration technique: the energy stability and the quality of the accelerated beams in terms of energy dispersion and emittance. The goal of the experiment underway at SPARC_LAB is to precisely solve these problems.
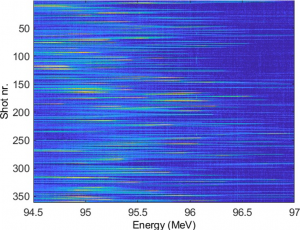
Figure 3 shows a series of measured energy spectra. The overall stability is 99.5% for an average energy of 95.7 MeV. The most interesting result is, however, related to the energy spread which is not degraded but conserved during the acceleration process.
This progress is of fundamental importance because it makes the accelerated beam in principle “usable” for applications such as, for example, Free-Electron Lasers (FEL). As soon as the experimental activity is resumed, the campaign of measures will continue also including the emission measure.
Given the recent approval of the funds for the EuPRAXIA@SPARC_LAB project, which involves the development of a new accelerator at LNF capable to drive a FEL using the beams accelerated by a plasma, these results represent an important milestone and a first demonstration that it is possible to take under control the quality of the beams produced by a plasma accelerator.
 INFN-LNF Laboratori Nazionali di Frascati
INFN-LNF Laboratori Nazionali di Frascati