It all started with Fritz Zwicky, who, in the early ’30s, undertook a systematic study of the Coma Cluster, a cluster of thousands of galaxies, about 20 million light-years wide, around 350 million light years away from Earth, in the direction of the constellation named Coma Berenices.
Zwicky performed two kinds of measure, which are the daily bread of astrophysicists: he estimated the total mass of the cluster by the number of galaxies he could see and by its total luminosity; then, by measuring the Doppler shift of the light emitted he determined the radial velocities – or along the line of sight – of the galaxies.
Starting from these data, Zwicky was able to calculate the total energy of motion (kinetic) and the gravitational one contained in the cluster. A famous theorem of Newtonian physics states that, in a closed system, like the cluster, the former must be half the latter. But Zwicky did not observe that. According to his measurements, the single galaxies moved too fast for the cluster to remain compact. With the velocities observed, the cluster should have “evaporated”: the galaxies would not have been seen clustered but escaping from each other.
To solve this paradoxical situation, Zwicky hypothesized the cluster contained also some invisible mass, that is a mass which exercises a gravitational pull but does not emit light, therefore not contributing to the galaxy luminosity. Zwicky coined the term “dark matter” to describe this invisible component he estimated to be at least 500 times the visible matter. Later, with the birth of X-ray astronomy, it turned out much of this “missing mass” was actually in the form of hot gases (powerful X-ray emitters) that contribute to the total mass of the galaxies much more than the visible stars. However, even taking into account the gases, a significant contribution was still missing to the total mass balance, about 5-6 times the one of the visible mass.
In the following 40 years after Zwicky’s observation, astronomers did not make any substantial progress in the study of this anomaly. Then, in the early ‘70s, Vera Rubin, with her collaborator Kent Ford, started to study the so-called rotation curves of spiral galaxies. A rotation curve is the behaviour of the rotational velocity in an astronomical system as a function of the distance from the centre of the system. The first rotation curve to be measured was the Solar System’s. Here the rotational velocity around the Sun, as evidenced by the motion of the planets, decreases as the square root of the distance from the Sun. The Solar System rotation curve is consistent with almost all the system mass located in the centre – the Sun – and with Newton’s law of universal gravitation. Indeed, we can consider this harmony as the first indication of validity of that law in the Solar System scale of distances.
Rubin expected to find the trend predicted by the Newton’s law of gravitation – represented by the red curve in figure 1. No way: in the galaxies, far beyond the visible mass, the rotational velocity at high distance from the galaxy centre is almost constant! (white curve in the figure).
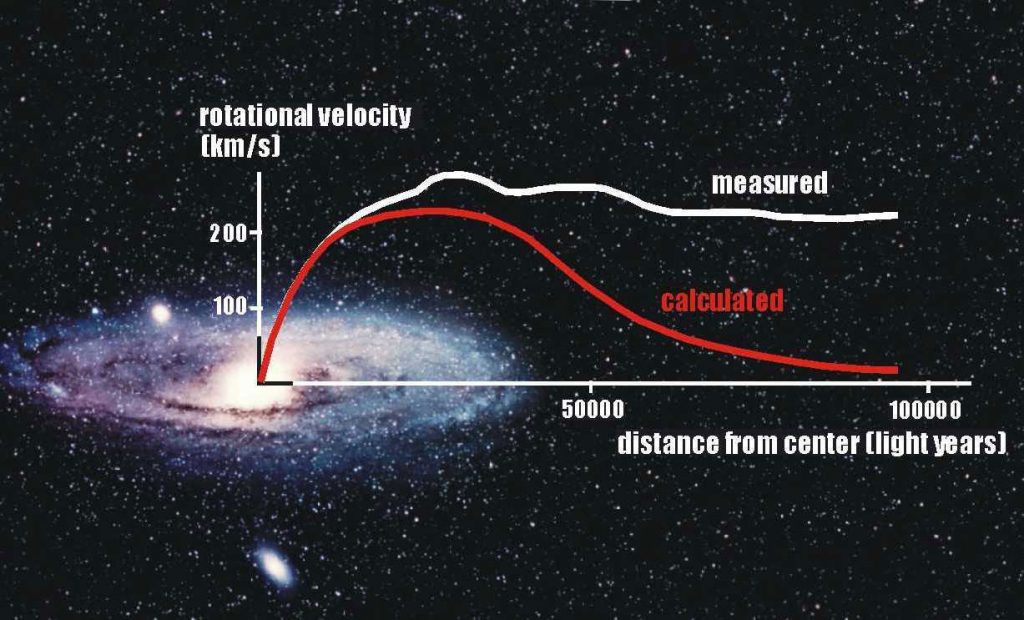
It is important to stress one thing. As you can see in the figure, the curve extends far beyond the region of the outermost stars. In this region rotational velocity is that of the ionized hydrogen clouds rotating around the galaxy centre. These clouds emit a radiation with a particular wavelength – the so-called Hα line with λ = 21 cm –, easy to detect. By the Doppler shift of this line Rubin was able to determine the orbital velocity of the outlying clouds.
In the framework of Newtonian Mechanics, the white curve in figure 1 can be understood only if the mass distribution extends far beyond that of the visible starlight, which is like saying the mass in the external regions of the galaxy is dark. This phenomenon is general: the rotation curve remains flat beyond the visible disk in almost every disk galaxy observed in sufficient detail. In the context of the dark matter hypothesis that means every galaxy is immersed in a wider dark component, a sort of halo within which this matter has a well-defined distribution: its density must decrease with the square of the distance from the galactic centre.
This is not the only “dark side” of the Universe. Unfortunately, there is another one, rather more disturbing, we cannot fail to mention. In 1998, two groups of astrophysicists, in the USA and in Australia, studying a particular category of supernovae, known as type Ia, explosed between 4 and 7 billion years ago, made a startling discovery: luminosity of far supernovae is, on an average, 25% smaller than what was expected.
It was quite quickly realized the only plausible explanation to this phenomenon was the following: far supernovae were further away than it has been thought. That can be fully explained if we admit in the past the Universe expanded slower than what can be deduced from its current expansion rate. In other words, the Universe is going through an expansion phase in which its evolution is dominated by a mysterious “dark energy”.
But let’s go back to the problem of dark matter; we will have the opportunity to discuss dark energy in more depth elsewhere. At present, two ideas – capturing different degrees of attention – have been around in the physics community.
Dark matter as particles
The easiest solution – and probably the most popular among physicists – to explain this evident mass deficit is to postulate the halo surrounding the galaxy is populated by elementary particles, electrically neutral, stable and massive, not yet observed. The fact that those particles are neutral explains why they are invisible, not being able to emit any electromagnetic radiation. They must be massive to justify their gravitational effects.
There are many good reasons supporting this “particle” hypothesis.
Firstly, we know regular matter, the one we experience everyday and we are made of, consists of well-determined elementary particles: those making up the so-called Standard Model. Every physical phenomenon we know is described at a fundamental level through the combinations of and interactions among those particles, according to the laws that have been confirmed – and still being confirmed – in the experiments. It is therefore reasonable to think the “dark world” repeats this corpuscular pattern of the regular matter too. In passing, we notice there are solid reasons – we are not going to debate now – to rule out the possibility dark matter is made of Standard Model particles.
The second reason is based on experience. In Physics, historically, several issues were solved by introducing new ad-hoc particles. Maybe the most famous example is the one of neutrino. In the ‘30s the analysis of some phenomena of radioactive decay showed an alarming inexplicable violation of the law of conservation of energy, stating the total energy in every isolated system remains constant whichever physical process is subjected to. In the mentioned processes, instead, a significant part of the initial energy seemed to come to nothing. So, the Austrian physicist Wolfgang Pauli hypothesized this energy was “taken away” by a very light neutral particle, with such elusive characteristics it could not be observed. Enrico Fermi started from Pauli’s idea and elaborated a rigorous theory for this kind of processes (the so-called beta-decays), naming the new mysterious particle “neutrino”. Fermi’s theory was so elegant and described with such precision the dynamics of beta processes that the existence of neutrino was accepted even in the absence of any direct evidence. It took more than two decades before the American physicists Frederick Reines and Clyde Cowan finally managed to capture some neutrinos produced by a nuclear reactor.
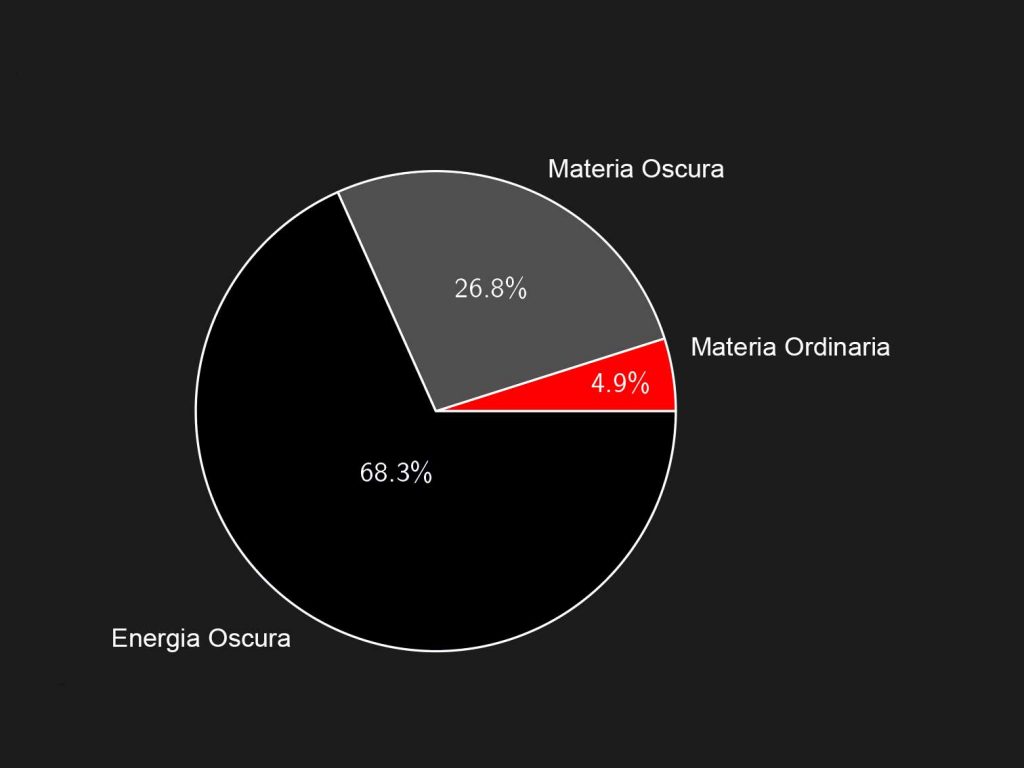
But the most convincing evidence supporting the particle nature of dark matter is cosmological. Actually, if during the formation of the cosmic microwave background (CMB) in the Universe there were just photons and regular matter, the present level of fluctuations in the CMB temperature distribution would be much bigger than the ones observed (ΔT/T ∼ 10$^{-5}$). The problem can be solved with the presence of dark matter which doesn’t couple directly to photons. The detailed study of fluctuations in the CMB temperature allows, additionally, to state dark matter accounts for about 25% of the present energy density of the Universe; with the addition of baryons, the total contribution of matter to the present density of the Universe reaches the 30% of the so-called critical density (∼ 5 hydrogen atoms per m$^3$), the density which makes the Universe geometry flat, as foreseen in the inflationary scenario. The rest is dark energy.
So, maybe the most amazing aspect of the Universe is that about 95% of its energy is made up of dark energy and matter: regular matter, the one making up our perceivable world, is nothing but a poor 5%.
Now, if dark matter is made of particles, it is acceptable to aspire to detect them, a result which – unfortunately – we have not achieved yet. The problem is that capturing these particles is more difficult than detecting neutrinos. This is because, while physical characteristics of the latter are perfectly defined by Fermi’s theory, which enables us to design ad hoc detectors to observe them, the same cannot be said for dark matter. Although some characteristics of these hypothetical particles are constrained by the need to respect observational facts described above, the range of potential candidates, in terms of mass and interactions with regular matter, is extremely wide. Thus, there is not just one experiment to verify all possible options.
In general, there are three fundamental lines of research. The direct observation of dark matter is based on the consideration the Solar System – and with it the Earth – rotating around the Galaxy centre continuously intercepts particles of the dark halo. To capture some of these particles suitable apparata are built and generally located in underground laboratories to minimize the environmental noise that would make the detection even harder. This line of research is carried out at INFN Gran Sasso National Laboratories, one of the main research centres of the world. Interestingly, because of the Earth’s revolution around the Sun, our planet moves sometimes in accordance and others in the opposite direction to the motion of the Solar System around the galactic centre (Fig. 3).
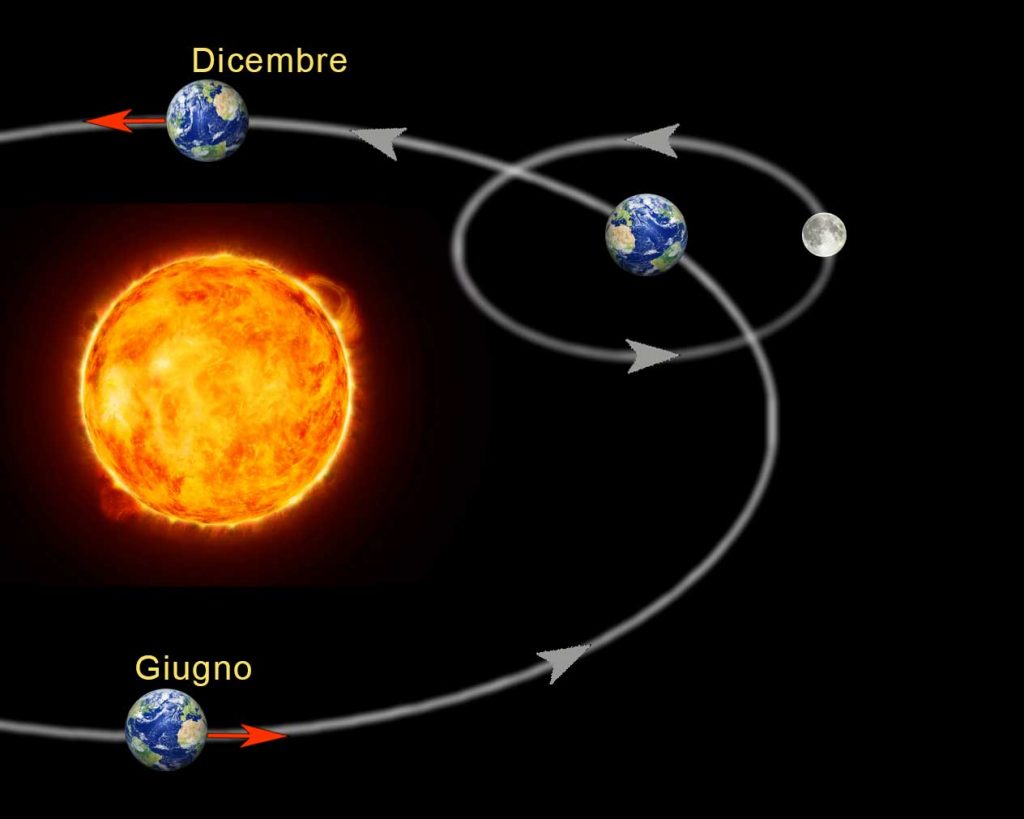
This should induce an annual modulation in the dark matter flux, with a peak around May and a maximum reduction around November, a phenomenon that may help to discriminate between true dark matter signals and other potential background signals.
Actually, the DAMA/LIBRA experiment at Gran Sasso has been observing for over a decade a signal with temporal characteristics compatible with that modulation. Despite the great interest in this experiment, we cannot yet be sure about this potential discovery since other experiments, which have – on paper – a sensitivity similar to that of DAMA/LIBRA, do not observe the same signal.
The indirect observation consists of looking for astrophysical signals attributable to interactions of dark matter particles between them or with ordinary matter particles. We can indeed hypothesize some mechanisms that – through those interactions – may produce, for example, photons with a well-defined energy which, if localized in space, could indicate specific clustering of dark matter. Usually this kind of research is performed by apparata on satellites launched in extra-atmospheric orbit, which have greater directional capability than the terrestrial ones.
Lastly, we can hope to produce dark matter by experiments in accelerators. In this case, generally, the signal to search for is an evident deficit in the energetic balance in the final state produced by the collisions, similar to the one due to the presence of neutrinos in beta-decays. The experimental challenge consists in being able to distinguish a true dark matter signal from all energetic deficits due to, e.g. simple (and inevitable) limitations in the apparatus resolution or to the production of neutrinos.
It should be pointed out once again that in all three cases examined above the signal to look for depends greatly on some a priori hypothesis somehow arbitrary about the physical characteristics of the particles searched. Particularly, there is no incontrovertible reason to exclude those particles have just gravitational interactions with the regular matter, which would make them – for all practical purposes – impossible to detect.
The hunt of these particles has been on for a long and continues, with increasingly powerful means.
The MOND paradigm
The hypothesis stating dark matter is composed of i.e. non-relativistic particles that interact only gravitationally – cold dark matter (CDM) – is satisfactory from the cosmological scale to the one of galaxies. This is where it faces difficulties.
Over the years, quite accurate simulations of the behaviour of systems composed of billions of particles interacting just gravitationally in an expanding Universe have been developed. These simulations provided a detailed description of the structure of the halos at all scales, from sub-galactic objects to big galaxy clusters. Below a certain distance from the centre, density becomes very high, i.e. there is a cusp; beyond, instead, density decreases pretty quickly with the distance from the centre, which, for long distances, translates into a rotational velocity slowly decreasing.
A decreasing velocity disagrees with the asymptotic flat trend of the rotation curves and may represent a confutation of the CDM hypothesis. Additionally, that inner cusp often does not fit with the rotation curves observed: the latter are generally more consistent with a halo having a core with constant density. Finally, simulations predict the existence of many sub-halos, the so-called satellite halos, much more than the ones actually observed around the spiral galaxies like the Milky Way.
From the start the constant asymptotic velocity seemed very strange to Mordechai Milgrom, the Israeli physicist who, in 1980, while thinking about this aspect, tackled the problem from an entirely different point of view. The need to add dark matter is just an inference of the Newtonian gravitational theory and, therefore, if we cannot predict constant curves, instead of creating a new category of matter, we should fix Newton. The modification suggested by Milgrom is simple: when the acceleration of a body becomes less than a certain critical value a$_0$, of the order of $~10^{-10}$ m/s$^2$ (100 billion times smaller than acceleration of gravity on the Earth), the force is no longer proportional to the acceleration (F = m a) – as stated by Newton’s second law – but rather to its square (F = m a$^2$/a$_0$). Hence the name MOND (“MOdified Newtonian Dynamics”) given to the corresponding theory.
The result of this modification is clearly evident in Fig. 4.
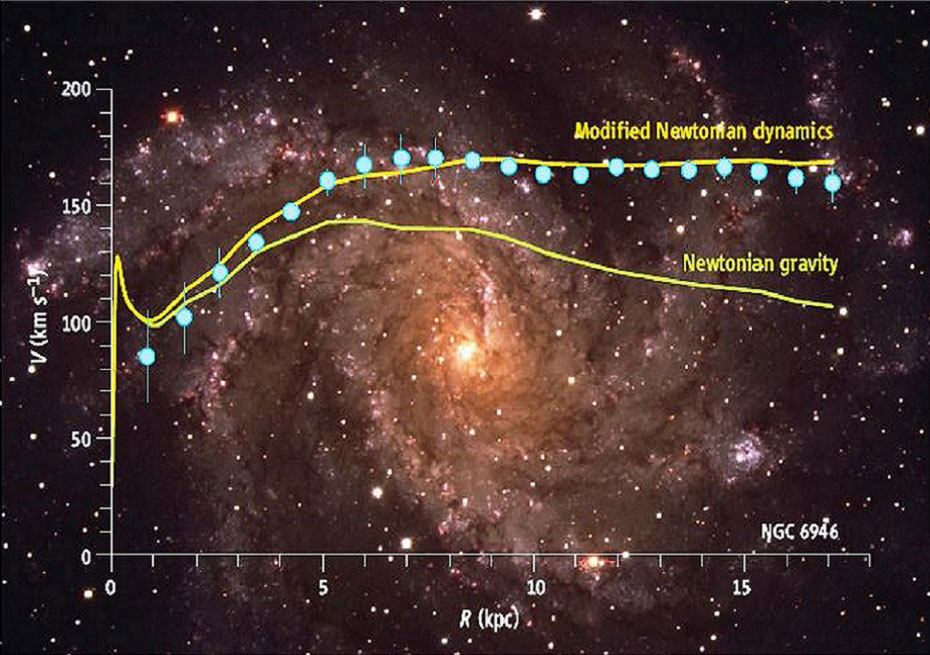
We should not get too excited about the correspondence with the experimental data: this theory was designed to replicate flat rotation curves. What’s really astonishing, if ever, is that the same value of critical acceleration works for a great number of galaxies.
However, there is an important aspect to be stressed. The observations show the constant value of the peripheral rotational velocity depends of the visible mass (the so-called baryonic mass) of the galaxy (Tully-Fisher relation). This correlation applies to different types of galaxies and baryonic masses: from small-mass dwarf galaxies, dominated by gases, to the massive big spirals with significant bulges in their centre. In the framework of the dark matter hypothesis, this aspect would imply an exact correlation between the baryonic mass of the relatively small object in the centre and the rotational velocity of particles moving in circular orbits in the wide outlying dark halo, a correlation that appears absolutely unnatural. In the MOND framework, this correlation is totally natural and regulated by a coefficient equal to the reciprocal of the product between the Newton’s gravitational constant G and the critical acceleration a$_0$. In principle, this acceleration is a parameter other than the one that determines the shape of the rotational curves. But, surprisingly, the observations lead to the same value for both. Although this phenomenology was already known before MOND’s formulation, there was no guarantee the value of a$_0$ necessary for replicating Tully-Fisher law had to do with the shape of rotational curves in the flat region. So, in the MOND context, a single formula unifies two key aspects of the spiral galaxy phenomenology.
At this point, we should ask ourselves: where does this critical acceleration come from? Can we identify a natural value for it? The remarkable thing is that the value of a$_0$ – taken from the study of galaxy rotation curves – is the same order of magnitude of the product between the speed of light and the current value of the Hubble constant. That brings us to hypothesize MOND could be an effect of the cosmological expansion on the dynamics of local systems.
Since we also found a possible origin of the critical acceleration, is everything okay with MOND? No, it’s not: from an empirical point of view, the theory has some problematic aspects, first of all the fact it cannot exhaustively describe the mass discrepancy in galaxy clusters. However, one thing we do know: it is possible to recover this phenomenology by spoiling – so to speak – the purity of MOND adding some particular “dark matter”, like, for example, ordinary neutrinos having a mass between 2 and 4 eV (we learned neutrinos have a mass different from zero in the early 1990s when, for the first time, the phenomenon of oscillation – a change of their nature while propagating –was observed; the problem is, from these measurements, we are able to determine only the square of the mass difference among the different types of neutrino), or “sterile” neutrinos (not completely interacting) with a mass in the order of 10 eV.
There are also some theoretical issues. The most pressing is that MOND, after more than 30 years from its formulation, still lacks an acceptable relativistic version. Without this extension, we cannot deal with cosmology and the question of structures formation, i.e. the large scale aspects where the standard paradigm, instead, works really well. Therefore, the study of the CMB falls outside the field of application of MOND.
In the last decade, several relativistic versions of MOND have been proposed, each of them potentially able to solve the cosmological problems. Many of those theories – among which the one by the Israeli physicist Jakob Bekenstein – require the introduction of additional fields, of a different nature than the gravitational one. These theories are more complicated – and less aesthetic– than the General Relativity and how they deal with cosmological aspects, such as the scale and distribution of CMB anisotropies, is still not fully clear. This kind of theories are interesting because they all request a change in Einstein’s theory, which, sooner or later, must come about. Actually we know General Relativity cannot be the ultimate answer to the problem of gravity. In fact, it contains the scariest nightmare of physicists: infinity! In the centre of a black hole; in the Big Bang at the beginning of the Universe. Most physicists think there is no reason to worry. These infinities come up when you apply the theory on a very short distance, where, inevitably, you need to consider Quantum Mechanics too. For this reason, many people have pinned their hopes on the cancellation of those divergences by the still elusive unification of General Relativity and Quantum Mechanics, i.e. the Quantum Gravity: the final theory in which the two pillars of XIX century physics, each giving away some of its characteristics, eventually will merge.
But it is not just the problem of singularities which tells us General Relativity cannot be the ultimate theory for gravitational interaction. It is the cosmological model itself, currently attracting more credit among physicists – ΛCDM: the cosmological constant (Λ) plus cold dark matter (CDM) – that requires going beyond General Relativity. As we have seen, it needs two additional sources, dark matter and energy, for which we have no evidence independent from astronomical observations, with density of energy fixed by these observations and that, at present, are mysteriously, almost the same.
In conclusion, we still have some questions. What is the solution to the enigma of “gravitational anomalies” we have been talking about? Dark matter on cosmic scale and modified dynamics on the galactic one? Is there any field acting like dark matter on large scale, but mimicking a modified dynamics on shorter scales? Can the phenomenology of dark matter, dark energy and MOND be unified in a single theory?
There are two diametrically opposed possibilities: there are dark matter particles but they cannot show their presence on the galaxy scale; there is no dark matter and the cosmic mass discrepancy is an aspect of MOND (in its relativistic extension) on large scale. Otherwise, the solution lies in something completely unimagined, on a deeper level and that, progressing the scale, fades from MOND to dark matter particles.
The ongoing experiments to detect dark matter particles and the future astrophysical/cosmological observations will shed light on this fascinating problem (D. Babusci, F. Bossi).
Translation by Camilla Paola Maglione, Communications Office INFN-LNF
 INFN-LNF Laboratori Nazionali di Frascati
INFN-LNF Laboratori Nazionali di Frascati