Fundamental interactions and their mediators
by Riccardo Barbieri
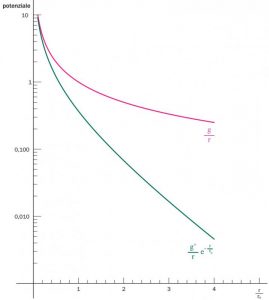
Gravitational interactions sharply entered into science when Newton, in 1687, formulated his famous law stating the attraction between two masses is proportional to their product and inversely proportional to the square of the separation distance between them. Almost a century later, Coulomb introduced an analogous law for the interaction between two electric charges, here again proportional to their product and inversely proportional to the square of their distance, which was the first step towards the interpretation of all the electromagnetic interactions. Why do we have to wait until the XIX century for the weak and strong interactions – also called nuclear – to step out on the stage of science, instead? The reason is clear: the different range of the respective forces. Gravitational and electromagnetic interactions are commonly said to have an infinite range, while the nuclear and weak ones have a finite range, beyond which the corresponding effects rapidly fade off. The characteristics of electromagnetic interactions can be described with the so-called “coulombian” potential, inversely proportional to the distance from the source (see fig. a). To the nuclear and weak interactions we can ascribe an analogous potential, though corrected with a term that decreases exponentially with the distance and depends on a characteristic length, r0, which determines the interaction range (see fig. a). This potential is called “yukawian”, named after the author who introduced it in the nuclear interaction context, whose range is about five orders of magnitude smaller than the typical radius of a hydrogen atom. Instead, nuclear interactions can have a range a thousand times bigger than the one of weak interactions. As we will see, the range is inversely proportional to the mass of the particle mediating the corresponding interaction. Neglecting the (extremely weak) gravitational interactions – which deserve a separate discussion and are, nevertheless, irrelevant in the elementary particle world – this difference between electromagnetic interactions on one hand and the nuclear and weak ones appears contrary to the current description of the interactions within the Standard Model.
In the Standard Model equations, the mediators of strong, electromagnetic and weak interactions, respectively gluons, the photon and the “intermediate bosons” W and Z, have a common nature. They are in any way spin-1 particles, or bosons, that intervene to give to the symmetries of the theory a local character, in other words independent from the space-time position. We are talking specifically about an apparent contrast, since in the fundamental equations all these bosons are massless, while the mass of the mediator is the key factor to determine the interaction range. As a matter of fact, the difference is in the different reaction to the quantum “vacuum” of the corresponding fields. It is obvious that the vacuum of the quantum field theory, or the lowest-energy state, is quite different from the “vacuum” we commonly refer to.
The quantum field theory vacuum is teeming with pairs of “virtual” particles produced from the interactions with the same field: for example, electron-positron pairs in the case of quantum electrodynamics (see. fig. b), quark-antiquark or gluon-gluon pairs in quantum chromodynamics (see. fig. c). It is one of the most surprising effects made possible by Heisenberg’s uncertainty principle.

The case of the electromagnetic field is shown in fig. b: the + – pairs spontaneously created from the “vacuum” orient themselves so as to “polarize” the vacuum itself, like in a dielectric material, tending to shield the opposite charged particle in the centre of the figure. Consequently, increasing the distance, the corresponding charge is gradually decreased. The impressive fact, theoretically discovered in 1973, is that the vacuum around the field of quarks, with “color” charge, behaves in the opposite way: the “color” of quarks, or of the same gluons, increases with the distance r. Therefore, while an electron and a positron normally attract each other yet can be moved apart by exerting a force decreasing with the distance, this is not possible with a pair of “colored” quark-antiquark. Moving apart from one another, the mutual attraction becomes so strong that it is energetically more convenient to tear from the “vacuum” another quark-antiquark couple and break the attraction potential chain. The peculiar scale of this phenomenon is called “confinement” scale inside the “hadrons”, whose total color is null.
That’s why we have never observed free quarks, and free gluons either. Among the others, the proton and the neutron are hadrons, whose mass is due to the confinement energy and, as such, are inversely proportional to the confinement scale. The interaction between protons and neutrons in a nucleus is mediated by the exchange of other hadrons, the lightest of which, the pion (also known as “π meson”), produces the longest-range strong interaction. The pion mass is around 8 times smaller than the proton one and the Yukawa potential range produced by the pion exchange is about 1 fermi yet, as mentioned above, a hundred thousand times smaller than the typical radius of a hydrogen atom. We wonder: don’t the W and Z bosons produce virtual particle pairs too? Yes of course, but the effect determining the weak interaction range is of a different nature and relatively more intense, even if it derives from the vacuum. This is the “Higgs field”, whose lowest-energy state permeates the entire space-time with a condensate of Higgs particles. As a consequence, every particle interacting with the Higgs field, acquire a mass which is directly proportional to the respective coupling. Among all the mediators we have been mentioning, only the W and Z ones couple with the Higgs field and then only them receive a mass from it, almost a hundred times bigger than the one of the proton. That’s why “weak” interactions are such. Comparing them with the electromagnetic interactions mediated by the photon, the relative couplings (indicated by g e g’ in fig. a) are fully comparable. What makes the difference is the mass of W and Z, that enter in the corresponding Yukawa potential and severely limit the weak interactions beyond a scale of around one thousandth of a fermi. Therefore, for nuclear physics or even more so for atomic physics, the effects of weak interactions can be considered as contact interactions, in other words at a null distance between the particles, for example between the proton and the electron in the hydrogen atom. In this limit, weak interactions are well approximated by the theory formulated by Fermi already in 1934. On the contrary, in experiments probing distances smaller than the range of weak interactions, as it is usually done at the Large Hadron Collider of Cern, we observe that the intensity of weak and electromagnetic interactions is comparable.
Translation by Camilla Paola Maglione, Communications Office INFN-LNF
 INFN-LNF Laboratori Nazionali di Frascati
INFN-LNF Laboratori Nazionali di Frascati