Nel corso degli ultimi decenni, una pletora di risultati sperimentali ha fermamente stabilito che i processi tra particelle elementari governati dalle interazioni forti sono correttamente descritti da una teoria nota come Cromodinamica Quantistica (QCD). Sebbene finora non ci siano risultati sperimentali che contraddicano le previsioni della QCD, questa teoria, insieme a una profonda comprensione di molte questioni fondamentali, propone anche un enigma teorico. La QCD dipende da due parametri fondamentali adimensionali il cui valore non è previsto dalla teoria, ma deve essere determinato sperimentalmente. Il primo, $α_{s}$, determina l’intensità delle interazioni ed il suo valore sperimentale si può considerare naturale per una quantità adimensionale (è dell’ordine dell’unità, sebbene il numero esatto dipenda dalla scala di energia a cui si misura a cui si misura $α_{s}$). Il secondo, θ, rappresenta l’entità della violazione della simmetria di carica-parità (CP) nelle interazioni forti. La teoria impone soltanto che il valore di θ, un parametro angolare, debba essere compreso nell’intervallo [-π, π], ed anche in questo caso sarebbe naturale aspettarsi un valore all’incirca dell’ordine dell’unità. Sorprendentemente, invece, si è trovato che il valore assoluto di θ deve essere inferiore a 10-10, così come si evince dagli stringenti limiti sperimentali sul momento di dipolo elettrico del neutrone, una quantità che viola la simmetria CP. Questo valore così piccolo viene considerato altamente innaturale per un parametro adimensionale, e sarebbe sicuramente più naturale se, per qualche motivo, risultasse θ = 0. Questo implicherebbe che la QCD è una teoria che conserva la simmetria CP, in accordo con le osservazioni.
Un elegante meccanismo per garantire θ = 0 è stato proposto nel 1977 da Roberto Peccei e Helen Quinn. Il meccanismo Peccei-Quinn (PQ) implica l’esistenza di una particella di spin zero e, in prima approssimazione, di massa nulla, comunemente nota come assione. Tuttavia, ci sono sottili correzioni al primo ordine, in conseguenza delle quali l’assione acquisisce una piccolissima massa $m_{a}$, presumibilmente ancora più piccola di quella dei neutrini. Subito dopo che il meccanismo PQ fu proposto, ci si rese conto che lo stesso fenomeno dinamico che spinge θ verso zero, genera nel vuoto una popolazione di assioni con quantità di moto nulla, e questi assioni dovrebbero oggi pervadere l’intero universo osservabile. È notevole che per un certo intervallo di masse dell’assione, compatibile con le aspettative teoriche, questo `mare’ di assioni potrebbe costituire la materia oscura cosmologica. Il fatto che gli assioni possano essere naturali candidati per la materia oscura aumenta l’interesse teorico verso il meccanismo PQ e giustifica i vari esperimenti di ricerca assioni in programma per il prossimo futuro.
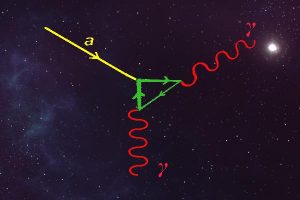
Una delle proprietà peculiari dell’assione è quella di interagire con una coppia di fotoni (vedi fig. 1). Malgrado l’intensità, $g_{aγγ}$, di questo accoppiamento dipenda dal modello, praticamente tutti gli esperimenti di ricerca in corso si basano sulla conversione di assione in fotoni mediata da questo accoppiamento. Chiaramente, l’obiettivo delle ricerche dell’assione è quello di coprire la regione nello spazio dei parametri (nel piano $g_{aγγ}$ – $m_{a}$) in cui si collocano i modelli realistici. Attualmente, tuttavia, i confini di questa regione sono fissati sulla base di criteri piuttosto arbitrari.
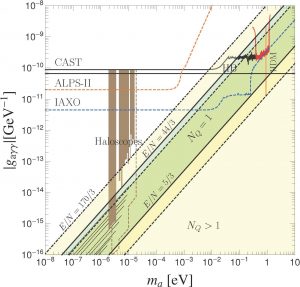
La quantità E/N determina l’intensità dell’accoppiamento assione-fotone e assume valori diversi nei differenti modelli.
Il problema di definire su una base fenomenologica più solida la regione all’interno della quale dovrebbero indirizzarsi le ricerche dell’assione è stato affrontato di recente da Luca Di Luzio (Durham University), Federico Mescia (Barcellona University) ed Enrico Nardi (LNF). I risultati di questa ricerca sono stati pubblicati in uno degli ultimi numeri della prestigiosa rivista Physical Review Letters e l’articolo è stato inserito tra quelli suggeriti dai redattori della rivista.
Gli autori hanno proceduto a classificare un ampio insieme di modelli di assione, scegliendo come fenomenologicamente preferiti quelli che non danno luogo a problemi cosmologici (sotto forma di reliquie cosmologiche stabili fortemente interagenti), e dove l’intensità delle interazioni tra le particelle note (ad esempio, leptoni e quark) non diviene infinita al di sotto dell’energia di Planck. Gli autori hanno identificato quindici casi che soddisfano questi criteri. Essi definiscono una regione fenomenologicamente preferita, delimitata dalle due linee continue in Fig. 2, etichettate E/ N = 44/3 ed E / N = 5/3. (Per confronto, racchiusa tra le due linee tratteggiate, è raffigurata anche la regione che è stata finora considerata come la più interessante). Combinando tra loro i quindici modelli, possono essere realizzate altre possibilità che ancora soddisfano le due condizioni imposte. Essi coprono la regione più grande, in giallo chiaro nella figura, che è delimitata dalla linea etichettata E / N = 170/3. All’interno di questa regione allargata, sono possibili accoppiamenti assione-fotone di quasi un ordine di grandezza più grandi. Tuttavia, in alcuni casi può anche accadere che l’assione si disaccoppi quasi completamente dal fotone, di modo che la regione non possiede un limite inferiore.
Si prevede che questa analisi contribuirà a indirizzare gli sforzi sperimentali per la ricerca dell’assione verso la regione dello spazio dei parametri che comprendono i modelli fenomenologicamente più interessanti.
L’articolo è liberamente disponibile al link: https://arxiv.org/abs/1610.07593 (Enrico Nardi)
 INFN-LNF Laboratori Nazionali di Frascati
INFN-LNF Laboratori Nazionali di Frascati